복습
- 가설(Hypothesis)

(단순 선형 회기의 경우)
(간략화한 경우)
- 비용 (Cost)
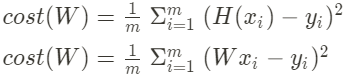
(MSE 방법)
(간략화한, 경우)
- 경사하강법(Gradient Decent Algorithm)

기울기가 줄어드는 방향으로 W를 업데이트 시키면서, cost가 최소가 되는 W를 찾는 가장 대표적인 방법.
다변수 선형 회기(Multi Variable Linear Regression)
특징(feature)이 여러 개인 선형 회기로 단일 선형 회기에 비해 예측력이 높다.
계산시, 변수가 많아질 수록 계산식이 복잡해지므로 행렬(Matrix)을 사용한다.
- 가설(Hypothesis)
변수가 n개이면 가중치도 n개가 필요하다.
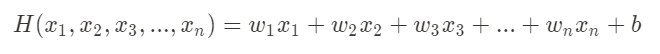
따라서 위와 같은 가설 함수가 생성된다.
하지만, 변수가 늘어날 수록 해당 수식 길고 복잡해지므로, 아래와 같은 행렬 값을 이용한다.

따라서, 행렬을 이용하여 가설을 간단히 나타내면 아래와 같다.

※ 이때 각 행렬의 크기는 H(X)가 [데이터 수, 출력 수], X가 [데이터 수, 요소 수], W가 [요소수, 출력수] 가 된다
.※ 단일 선형 회기와 이론적 설명에서는 W가 계수, x가 변수이므로 H(x) = Wx + b 와 같이 표현하지만, 다중 선형 회기와 실제 TensorFlow 코드에서는 위와같은 행렬 값을 이용하기 위해, H(X) = XW 로 사용한다.
실습1 : 기존 방법과 행렬을 이용한 방법 비교
아래는 퀴즈1, 퀴즈2, 중간고사 성적으로 기말고사 성적을 예측하는 것이다.

행렬을 이용하지 않은 경우,
코드
import tensorflow as tf
learning_rate = 0.00001
#변수마다 각각의 데이터셋을 지정
x1 = [73., 93., 89., 96., 73.]
x2 = [80., 88., 91., 98., 66.]
x3 = [75., 93., 90., 100., 70.]
y = [152., 185., 180., 196., 142.]
w1 = tf.Variable(10.0)
w2 = tf.Variable(10.0)
w3 = tf.Variable(10.0)
b = tf.Variable(10.0)
#Gradient Descent 적용
n_epochs = 1000
for i in range(n_epochs+1):
with tf.GradientTape() as tape:
hypothesis = w1 * x1 + w2 * x2 + w3 * x3 + b
cost = tf.reduce_mean(tf.square(hypothesis - y))
w1_grad, w2_grad, w3_grad, b_grad = tape.gradient(cost, [w1, w2, w3, b])
w1.assign_sub(learning_rate * w1_grad)
w2.assign_sub(learning_rate * w2_grad)
w3.assign_sub(learning_rate * w3_grad)
b.assign_sub(learning_rate * b_grad)
if i % 100 == 0:
print("{:5}|{:10.6f}".format(i, cost))

행렬을 이용할 경우,
코드
import tensorflow as tf
import numpy as np
learning_rate = 0.00001
#전체 데이터를 한 번에 가져와 사용할 수 있다.
data = np.array([
#x1, x2, x3, y
[73., 80., 75., 152.],
[93., 88., 93., 185.],
[91., 91., 90., 180.],
[96., 98., 100., 196.],
[73., 66., 70., 142.]
], dtype = np.float32)
#독립변수와 의존변수 분리
X = data[:, :-1]
Y = data[:, [-1]]
W = tf.Variable(tf.random.normal([3, 1]))
b = tf.Variable(tf.random.normal([1]))
#Gradient Descent 적용
n_epochs = 1000
for i in range(n_epochs+1):
with tf.GradientTape() as tape:
hypothesis = tf.matmul(X, W) + b
cost = tf.reduce_mean(tf.square(hypothesis - Y))
W_grad, b_grad = tape.gradient(cost, [W, b])
W.assign_sub(learning_rate * W_grad)
b.assign_sub(learning_rate * b_grad)
if i % 100 == 0:
print("{:5}|{:10.6f}".format(i, cost))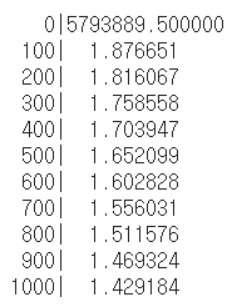
둘 다 동일한 결과를 보이지만, 행렬을 사용하지 않았을 경우, 데이터 셋 값을 변수에 따라 일일이 지정해줘야하며, Gradient Descent Algorithm에서도 가설과 가중치 업데이트 부분을 일일이 작성해줘야한다는 면에서 불리하다.
실습2 : 집 값 예측하기
아래 주소의 캐글에서 워싱턴 주의 킹 카운티 지역의 집 값에 관한 데이터 소스를 다운 받는다.
https://www.kaggle.com/divan0/multiple-linear-regression
먼저, 위에서 다운 받은 csv파일을 colab에 업로드 한 뒤, 데이터 분석을 위한 라이브러리인 pandas를 통해 데이터를 불러온다.
import pandas as pd
fileLoc = "/content/kc_house_data.csv"
data = pd.read_csv(fileLoc)
#데이터 요약본 보기
data.head
#데이터 타입 출력
print(data.dtypes)
데이터를 잘 받아왔으면, 전체 데이터 셋을 8 : 2로 학습(train)을 위한 데이터와 모델 시험(test)을 위한 데이터로 나눈다. 이때, 집 가격을 평가할 요소는 x에, 요소들로 부터 구할 값인 집 가격은 y로 지정한다.
from sklearn.model_selection import train_test_split
x = data[['bedrooms', 'bathrooms', 'sqft_living', 'sqft_lot', 'floor', 'view', 'condition', 'yr_built']]
y = data[['price']]
x_train, x_test, y_train, y_test = train_test_split(x, y, train_size=0.8, test_size=0.2)
이제 모델을 생성해볼 차례이다. 간단하게 Scikit-Learn 라이브러리를 이용하여 모델을 생성한다.
# 모델 생성
from sklearn.linear_model import LinearRegression
#선형 회기 객체 생성
mlr = LinearRegression()
#트레이닝 셋으로 학습
mlr.fit(x_train, y_train)
#회기 계수 출력
print(mlr.coef_)
모델이 생성되었으면, 테스트 데이터 셋을 이용하여 해당 집 가격을 예측해본다.
또한, 모델이 잘 생성되었는지 판단하기 위해, 실제 집 가격과 비교하여 산점도를 플롯시켜 본다.
import matplotlib.pyplot as plt
#테스트 셋으로 예측값 생성
y_predict = mlr.predict(x_test)
#예측값과 실제값을 산점도 플롯
plt.scatter(y_test, y_predict, alpha=0.4)
#실제 가격
plt.xlabel("Actual price")
#예측 가격
plt.ylabel("Predicted price")
#다중선형회기를 통한 집 값 예측
plt.title("MULTIPLE LINEAR REGRESSION")
plt.show()
이렇게 생성한 모델을 가지고, 임의의 조건 값들을 넣어 집 값을 예측할 수 있으며, 또한 어떤 요소가 집 값에 영향을 미치는지 비교할 수 있다.
# 임의 조건으로 집 생성
my_apartment = [[3, 1, 1067, 3558, 1, 2, 4, 2000]]
# 위의 조건 시 집 가격 예측
my_predict = mlr.predict(my_apartment)
# 예측 집 값 출력
print(my_predict)
'bedrooms', 'bathrooms', 'sqft_living', 'sqft_lot', 'floor', 'view', 'condition', 'yr_built' 조건이 3, 1, 1067, 3558, 1, 2, 4, 2000 값과 같으면 예상되는 집 값은 약 258901 이다.
# 주택의 면적 'sqft_living'과 가격 'price'의 관계
plt.scatter(data[['sqft_living']], data[['price']], alpha=0.4)
plt.show()
# 건설 연도 'yr_built'와 가격 'price'의 관계
plt.scatter(data[['yr_built']], data[['price']], alpha=0.4)
plt.show()
위 결과로 보아 주택의 면적은 가격과 비례하며, 건설 연도는 크게 영향을 미치지 않는다.
'AI' 카테고리의 다른 글
| [ai-2team]1. Linear Regression, minimize cost (0) | 2021.01.07 |
|---|---|
| [ai-1team] 5. Convolutional Neural Network (0) | 2021.01.01 |
| [AI-3Team] Logistic Regression (0) | 2020.12.27 |
| [ai-1team] 4. 딥 네트워크 학습 및 코드 실습 (0) | 2020.12.22 |
| [ai-3team] Study_2: Linear Regression and Optimization (0) | 2020.11.26 |



