Logistic Regression
Classification
Binary Classification은 어떠한 데이터를 두가지(Yes/No, 1/0)로 나누는 것이다.
Logistic vs Linear

Logistic은 이산적인 데이터를 말한다. 예를 들어 신발 사이즈, 회사의 사람 수, 자녀의 수, 교통사고 발생 건수 등을 예로 들 수 있다.
Linear는 연속적인 데이터를 말한다.시간, 몸무게, 키 등 원칙적으로는 무한히 작은 단위로 측정이 가능하고 실수값을 취할 수 있는 데이터이다. 수치 사이에 틈이 없다.
예를 들어 무게, 온도, 부피, 투자 수익률 등이 있다.
Sigmoid(Logistic) function


합격 불합격이 있는 시험에서 공부 시간에 따라 합격 불합격을 예측한다고하자. Linear Regression을 사용하면 예측값들은 연속적인 실수값이 나올 것이다.
이는 우리가 원하는 결과가 아니기 때문에 새로운 함수가 필요하다.
새로운 함수로 Sigmoid 함수를 이용한다.
sigmoid함수는

으로 나타낸다.

이렇게 생긴 그래프로 y절편은 0.5이고 상한선은 1, 하한선은 0이다.
이 때, 0.5를 Decision Boundary로 사용한다.
Logistic Regression의 가설함수는

로 나타낸다.
기존의 선형회귀의 가설함수를 정의역으로 사용한다.

tf.math.sigmoid메소드는 y = 1 / (1+exp(-x))를 계산하는 메소드이다.
tf.exp(x) 는 자연상수 e^x이다.
2번째 tf.div(1., 1.+tf.exp(z))에서 exp의 파라미터로 -z를 넣지 않은 것은, y축 대칭이동하면 Decision Boundary는 같고, 결과 값만 바뀌는데 결과 값은 classification에서는 크게 의미가 없어서 그런 것 같다.
Decision Boundary

predicted = tf.cast(hypothesis > 0.5, dtype=tf.int32)
⇒ 조건에 따라 true→1, false→0을 반환한다. 즉, 가설함수가 0.5(Decision Boundary)이상이면 1을 반환한다.
Cost Function

비용이 가장 적어지는 가설함수는 오른쪽과 같은 경우이다.
Logistic Regression에서 비용함수를 선형회귀와 같이 (예측값-실제값)^2의 평균으로 계산하면 비용함수가 구불구불하게 나온다.


이렇게 되면 경사하강법으로는 local minimum과 global minimum을 구분할 수 없다.
그래서 로그함수를 사용한다. log를 사용하는 이유는 자연상수 e에 대한 값을 처리하기 위해서이다.

로지스틱 함수의 cost function은 이와 같이 나타낸다. 코드로 나타낼 경우 if문을 항상 써야하기 때문에

처럼 사용한다.
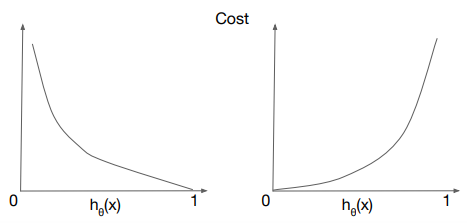
위의 그래프를 보자.
왼쪽의 그래프가 y=1일때의 그래프이다. 이 때, 예측값인 h(x)가 1에 가까워질수록 Cost가 줄어든다. 반대로 0에 가까워지면 양의 무한대로 발산한다.
오른쪽의 그래프는 y=0일 때의 그래프이다. 예측값이 0에 가까워질수록 Cost가 줄어드는 것을 볼 수 있다.
Optimization
optimization은 비용함수가 최소가 되는 지점을 찾는 방법을 말한다. 이 강의에서는 Gradient Descent를 사용한다.


Logistic Regression은 이와같은 일련의 과정으로 동작한다.
데이터를 선형함수에 취한 값을 logistic function(sigmoid)에 입력시키고 Decision Boundary를 통해 0또는 1로 분류를 한다.
+α
머신러닝은 regression과 classification으로 나눠지는데, 왜 classification에서 logistic regression이 나오는가?
⇒ 많은 글에서 logistic regression과 logistic classification을 혼재하여 사용하고 있다.
⇒ 내가 생각하기에 logistic regression은 classification의 구현 방법중 하나인 것 같다. 선형회귀로는 연속적인 값들을 분석, 예측하고, 로지스틱으로는 이산적인 값들을 분석 예측하는데 적합하기 때문에 classification에서 사용하는 것이라고 이해했다.
로지스틱(Logistic) 회귀분석은 회귀분석이라는 명칭과 달리 회귀분석 문제와 분류문제 모두에 사용할 수 있다.
Logistic Regression은 Classification 알고리즘 중에서도 정확도가 높은 알고리즘으로, Deep Learing에서 기본 Component로 사용된다.
Logistic Regression은 데이터의 특성과 분포를 나타내는 최적의 직선(Linear Regression)을 찾고, 그 직선을 기준으로 분류(Classification)하는 것이다.
Logistic Regression에서 예측단계
1. 모든 속성(feature)의 계수(coefficient)와 절편(intercept)를 0으로 초기화한다.

2. 각 속성들의 값에 계수를 곱해서 log-odds를 구한다.

- ex) 0,7 ⇒ odds=0.7/0.3=2.33

- logistic regression에서는 속성(x)들에 계수(w)를 곱하고 b를 더해서 최종 log-odds를 구해야한다. 이 과정에서 행렬 곱을 사용하여 log-odds를 구한다.


- logit 함수는 정의역이 0과 1 사이이고, 단조함수, 연속함수이다.
- p는 확률로 0~1사이의 값을 갖지만, logit변환으로 음의무한대에서 양의 무한대까지 나타낼 수 있다.

- 이 logit함수의 역함수가 logistic함수이다. 치역이 0과 1사이이고 이 역시, 단조함수, 연속함수이다.

손실함수 유도

실습
Logistic Regression 예제
Titanic data 분석
참고자료
로지스틱회귀(Logistic Regression) 쉽게 이해하기 - 아무튼 워라밸
Logistic Regression은 왜 Linear Method라고 불리는가?
'AI' 카테고리의 다른 글
| [ai-1team] 5. Convolutional Neural Network (0) | 2021.01.01 |
|---|---|
| [AI-3Team] 다변수 선형 회기(Multi Variable Linear Regression) (0) | 2020.12.29 |
| [ai-1team] 4. 딥 네트워크 학습 및 코드 실습 (0) | 2020.12.22 |
| [ai-3team] Study_2: Linear Regression and Optimization (0) | 2020.11.26 |
| [ai-1team] 3. Application & Tips (0) | 2020.11.21 |



