안녕하세요 Sooss입니다. 드디어 AI 첫 스터디가 시작되었네요 엄청 어려워 보이지만 차근차근하다보면 언젠간 정복할 수 있지 않을까 하는 생각을 하며 글을 써보겠습니다. 오늘은 선형 회귀에 대하여 공부해보겠습니다.
Simple Linear Regression
Regression이란? "전체의 평균으로 되돌아간다."라는 의미입니다.
그래서 Linear Regression을 한마디로 정의하면 데이터를 가장 잘 대변하는 직선의 방정식을 찾는것이라고 말할 수 있습니다. 수식으로 표현하자면 y=ax+b 직선 방정식에서 a,b값을 구하는것이다라고 말할 수 있겠습니다.
Hypothesis(가설) 함수를 H(x) = Wx + b라고 가정하겠습니다.

다음과 같은 H(x)가 있습니다. 우리는 이 선이 이 데이터(파란색 점)들을 잘 대변하고 있다라고 가정합니다.
그러면 H(x)-y (빨간색) 값이 작을수록 데이터들을 잘 대변하고 있다고 표현 합니다.
그렇다면 우리의 목표는 H(x)-y (cost) 를 최소화 시키는 것입니다.
다음으로 넘어가기 전에 잠깐 알아야 할것이 저기 빨간색 부분을 보시면 뺄셈을 했을때, 어떤 부분은 +, 어떤 부분은 - 값이 나오게 됩니다. 따라서 우리는 최소비용함수를 만들때 제곱해야한다는 사실을 깨달을 수 있습니다.
Simplified Hypothesis
가설을 간략화 해보겠습니다.
H(x) = W(x)로 하고 그렇다면 cost는
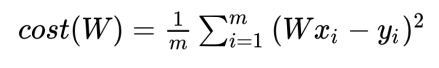
이렇게 됩니다.
cost(w)값은 어떻게 되느냐? w값을 변화시켜가며 지켜보면 됩니다.

x축은 W이고 y축은 cost(W)입니다. 여기서 cost가 가장 작게되는 w값을 구하면 됩니다.
사람은 쉽게 구별이 가능하지만 컴퓨터는 어떻게 구할까요? 컴퓨터가 최저점을 찾는 알고리즘이 바로
Gradient Descent(경사 하강법) 알고리즘 입니다.
How it works?
경사 하강법은 어떻게 동작할까요? 방법은 다음과 같습니다.
1. (0,0)에서 시작하고 다른값도 가능합니다.
2. cost가 줄어드는 방향으로 w, b값을 업데이트 합니다.
3. 이 과정을 최소점에 도달했다라고 판단될때까지 반복합니다.
알고리즘은 이렇고 그럼 Gradient를 구해야 하는데 이건 어떻게 구할까요? 바로 미분을 해서 구합니다. 미분을 구하기 위해 식을 살짝 수정합니다.

우선 분모는 1 / 2m으로 수정했습니다. 저기서 2로 하든 3으로하든 뭘로 나눠도 cost에는 영향이 미치지 않기 때문에 임의의 수를 줬습니다. 하지만 미분을 하면 저기 있는 2가 앞으로 빠져나와서 약분이 되기 때문에 2로 설정하였습니다.

따라서 최종 수식은 이렇게 됩니다. 여기서 알파값은 learning rate를 뜻합니다.
Multi Variable Linear Regression
하나의 변수보다는 여러개의 변수를 사용하는것이 예측하는데 도움이 되겠죠??

다변수 선형회귀는 다음과 같이 가중치를 둡니다.
그래서 이를 Matrix(행렬)로 표현하면

위와 같이 표현할 수 있습니다.
행렬 곱셈이 되려면 앞 행렬의 열과 뒷 행렬의 행의 개수가 일치 해야하는건 알고 계시죠? 😁
그러면 [n, 3], [3, 1]의 행렬이 있다고 가정합시다. 그럼 여기서 알 수 있는 부분은 무엇일까요?
먼저 결과 값은 [n, 1]이 출력될것입니다.
그 다음에 알 수 있는 부분은 앞 행렬의 행(데이터의 개수)은 몇개가 오든 상관없다 라는것을 알 수 있네요.
그럼 이제 소스코드로 지금까지 한 것을 보겠습니다 :)
Cost function in pure Python
import numpy as np
x = np.array([1, 2, 3])
y = np.array([1, 2, 3])
def cost_func(w, x, y):
c = 0
for i in range(len(x)):
c += (w * x[i] - y[i]) ** 2
return c / len(x)
for feed_w in np.linspace(-3, 5, num=15):
curr_cost = cost_func(feed_w, x, y)
print("{:6.3f} | {:10.5f}".format(feed_w, curr_cost))
파이썬으로 cost함수를 구현한 것입니다. 그냥 그대로 옮긴거라서 쉽게 이해하실겁니다.
다음은 결과값입니다.

Cost function in Tensorflow
위 식을 Tensorflow로 구혆한 코드입니다.
import numpy as np
import tensorflow as tf
x = np.array([1, 2, 3])
y = np.array([1, 2, 3])
def cost_func(w, x, y):
hypothesis = x * w
return tf.reduce_mean(tf.square(hypothesis - y))
w_values = np.linspace(-3, 5, num=15)
cost_values = []
for feed_w in w_values:
curr_cost = cost_func(feed_w, x, y)
cost_values.append(curr_cost)
print("{:6.3f} | {:10.5f}".format(feed_w, curr_cost))
Gradient descent
import numpy as np
import tensorflow as tf
x = np.array([1, 2, 3])
y = np.array([1, 2, 3])
x_data = [1.0, 2.0, 3.0, 4.0]
y_data = [1.0, 3.0, 5.0, 7.0]
w = tf.Variable(tf.random.normal([1], -100.0, 100.0))
for step in range(300):
hypothesis = w * x
cost = tf.reduce_mean(tf.square(hypothesis - y))
alpha = 0.01
gradient = tf.reduce_mean(tf.multiply(tf.multiply(w, x) - y, x))
descent = w - tf.multiply(alpha, gradient)
w.assign(descent)
if step % 10 == 0:
print("{:5} | {:10.4f} | {:10.6f}".format(step, cost.numpy(), w.numpy()[0]))
* 텐서플로우 버전땜에 그런가 실행이 안되네요..
w = 5, 알파값을 0.01로 두고 실행한 결과 값입니다.
w가 1로 수렴하는것을 알 수 있네요.

Hypothesis using matrix
import numpy as np
import tensorflow as tf
data = np.array(
[
[73.0, 80.0, 75.0, 152.0],
[93.0, 88.0, 93.0, 185.0],
[89.0, 91.0, 90.0, 180.0],
[96.0, 98.0, 100.0, 196.0],
[73.0, 66.0, 70.0, 142.0],
],
dtype=np.float32,
)
# slice data
x = data[:, :-1]
y = data[:, [-1]]
w = tf.Variable(tf.random.normal([3, 1]))
b = tf.Variable(tf.random.normal([1]))
learning_rate = 0.000001
# hypothesis, prediction function
def predict(x):
return tf.matmul(x, w) + b
# 실행 횟수
n_epochs = 2000
for i in range(n_epochs + 1):
# 비용함수의 gradient를 기록한다.
with tf.GradientTape() as tape:
cost = tf.reduce_mean((tf.square(predict(x) - y)))
# w, b를 각각 할당한다.
w_grad, b_grad = tape.gradient(cost, [w, b])
# 파라미터를 업데이트 한다.
w.assign_sub(learning_rate * w_grad)
b.assign_sub(learning_rate * b_grad)
if i % 100 == 0:
print("{:5} | {:10.4f}".format(i, cost.numpy()))
predict함수에서 보시면 하드코딩 할 필요없이 저렇게 곱하기만하면 끝나는것을 알 수 있습니다.

결과는 이렇게 나온다고 하는데 버전이 안맞아서 실행이 안되네요 ㅠㅠ
해결 방법을 찾아봐야겠습니다
오늘은 여기까지 😀
* 모두를 위한 딥러닝 시즌2 - Tensorflow강의를 참고하였습니다.
* 11.17 추가
============== Gradient Descent부분 ==============
gradient = tf.reduce_mean(tf.multiply(tf.multiply(w, x) - y, x))============== Gradient DescentHypothesis using matrix 부분 ==============
w = tf.Variable(tf.random.normal([3, 1]))
b = tf.Variable(tf.random.normal([1]))
* Thanks EunsungAhn
'AI' 카테고리의 다른 글
| [ai-1team] 4. 딥 네트워크 학습 및 코드 실습 (0) | 2020.12.22 |
|---|---|
| [ai-3team] Study_2: Linear Regression and Optimization (0) | 2020.11.26 |
| [ai-1team] 3. Application & Tips (0) | 2020.11.21 |
| [ai-1team] 2. Logistic Regression (0) | 2020.11.13 |
| [ai-3team] 2020-11-05 study (0) | 2020.11.06 |



